集積研での実験に関する説明動画を追加しました。
「実験技術・研究の覚え書き」カテゴリーアーカイブ
NI PXI-1031システム再始動
8年ほど前に購入したNI-PXIシステム
PXI-1031(箱)
PXI-6132(AD変換ボード)
を新しい測定に使うために、PCI接続ボードPCIe-8361を備えた別のPCに接続しようとするも、NI MAXで認識しない。
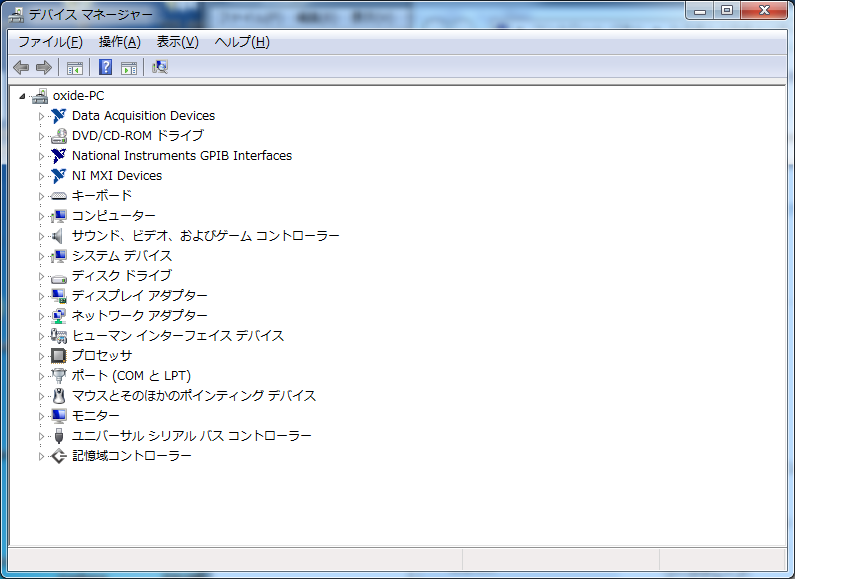
Windowsのデバイスマネージャーを見ても、それらしいデバイスマネージャーは見つからず、PCIボードが認識されてなさそうということがわかる。
LEDは点灯しているので、完全に壊れているわけではなさそうだが、とにかく認識しない。
いろいろ調べていくと、使用しているDell Optiplex 980は別のPCIeスロットを備えていることがわかり、そちらに差し替え。
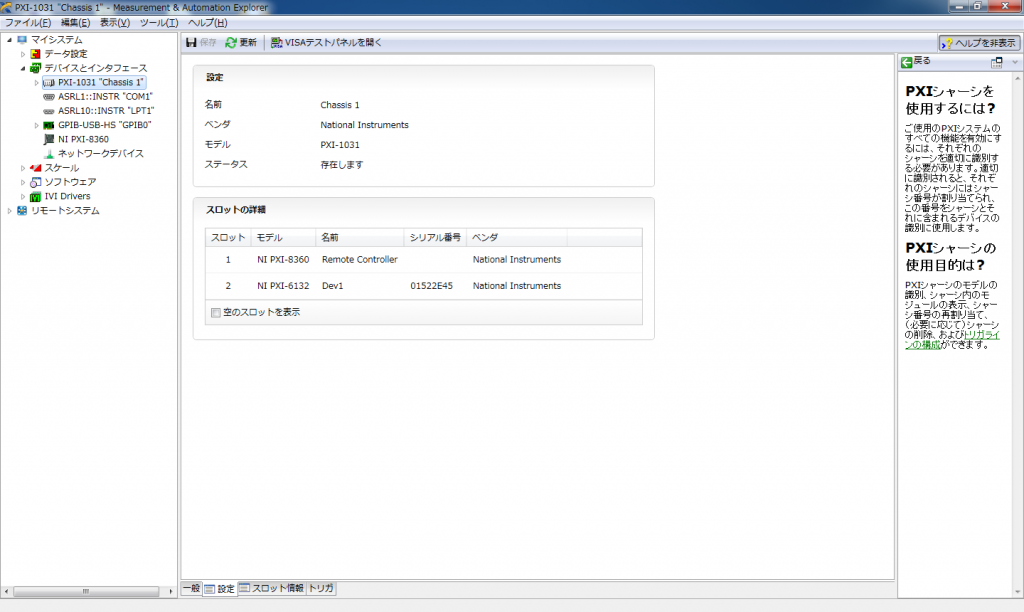
再起動すると、PCIe-8361がデバイスマネージャーに認識され、NI MAXでも装置が認識されました。
これで無事にIV特性測定の新しいシステムができそうです。
住友電工がBi系超伝導体を使用したコンパクトな超伝導マグネットシステムを発売
先日、住友電工からメールが配信され、ビスマス系超伝導体を用いたコンパクトなマグネットが発売されるとの情報を得ました。
http://www.sei.co.jp/super/magnet_coil/system.html#6t
今回当社が開発した冷凍機冷却型超電導マグネットシステム本体は、質量を100kgと従来システム本体の1/4まで軽量化し、寸法も奥行0.8m、幅0.3m、高さ0.3m と、同様に1/5まで小型化することに成功しました。また本システムは、永久磁石の検査工程中の磁化特性測定等への適用を視野に入れて開発したシステムで、B-Hカーブトレーサ、振動試料型磁力計(VSM)、ハードディスク検査装置等に加えて、磁場中熱処理炉等の製造装置への適用も可能です。
質量が100kGで最大磁場が6Tというコンパクトさも素晴らしいですが、特筆すべきは、30秒で6Tまで上げられることですね。
通常の超伝導コイルはNbTiを使っており、磁場の均一性を高めるなどの理由により自己インダクタンスが大きく、磁場スイープには時間がかかっていました。
高温超伝導体を使うことで、液体ヘリウムがなくても強磁場が出せるというのは、新興諸国の研究や産業の発展に大きな力になることと思います。
Nature Physicsにヘリウム不足の記事
Nature Physicsにヘリウム不足に関する記事を見つけました。
The impact of helium shortages on basic research
Nature Physics 10, 467–470 doi:10.1038/nphys3018
研究者向けの非常に詳細な情報があって、これを読んだだけで、情勢がわかる記事だと思います。
カタールの2014年世界シェアが14%にもなると予想されているのは、驚きです。
私が登場した3月の日経新聞の記事「ヘリウム危機 超えゆく技術」に関しては、いくつかのブログが言及しています。中には、すこしエキセントリックな主張のものまでありましたが・・。また、Nikkei Asian Reviewというサイトに海外向けの要約記事がありました。
No one taking helium shortage lightly
こちらには、私の写真を採用していただいております。(卒業生が見つけたというのは、これだったのか???)
BOMEM DA3
遠赤外分光器Bomem DA3(カナダ製)を廃棄することになりました。
高温超伝導発見直後の1989年ごろに購入した装置で、きわめて高分解能(0.3 GHz)のFTIR装置です。
国内にもまだ使用している研究室がありそうなので、パーツとして役立てないかと思い、取り扱いの業者に連絡したところ、引き取りたいとの連絡を頂きました。
遠赤外の天文関係の研究室とか、テラヘルツ光源を開発している研究室ではまだ使用されているそうです。
我々も、テラヘルツの研究を始めたときに使用することを検討しましたが、光源の水銀ランプが頭上の高い位置にあるので、クライオスタットを使う高温超伝導テラヘルツ光源への使用は断念しました。。
スキャンチューブを含めて、ほとんどのパーツを引き取って頂けるようで、ちょっといい事をした気分です。
スピン角運動量
Silver pastes
Dupont 4922 (or 4929)
- もっとも汎用性の高い銀ペースト。室温で硬化し、すぐに導通が確認できる。
- 接着力はほとんど無い
- 銀の粒径が小さい(1ミクロン程度)
- データシートによると、溶剤は酢酸ブチルとなっているが、酢酸ブチルセロソルブを併用すると硬化時間が調整できて、作業性が高くなり、小さな場所にも付けられる。
- 4929の方が若干粘性が高いが、溶剤次第ではある。
- メーカーデータシート
Dupont 6838
- 加熱硬化型銀ペースト。
- バインダ-となっているエポキシを150-300度で加熱重合させ、強い接着力を維持する。
- 銀の粒径は4922などと同様小さい。
- 溶剤は酢酸ブチルセロソルブ。室温ではほとんど硬化しないので、小さい場所にも付けられるが、加熱する必要がある。
- データシートは4922と同一
Epotek H20E
- 2液型加熱硬化銀ペースト。
- AB剤を等量混合させ、250度以上で加熱硬化させる。
- 350度の硬化により酸化物の大気暴露された表面にほぼ確実にコンタクトがとれる。
- 銀の割合が最も多そうな印象
- 粒径が粗く、実体顕微鏡でも銀の粒子がよく見える。
- メーカーデータシート
銀ペーストによる電極付けのコツ
- まず、午前中に始める
- 初めの1回目がもっとも精度が高い
- スライドガラスに取り出し、溶剤を加えて粘度を調整しながら、精神集中
- 爪楊枝の先に銀ペーストを取り、顕微鏡の視野内におく
- なるべく細い金線をピンセットでつかみ、顕微鏡の視野内にある銀ペーストを拾う
- ためらわずに目的の場所におく
- 動きのぶれを抑えるためには、ピンセットを持っていない方の手の指でピンセットの先を支える
- さらに精度が必要なときには、目的の場所になるべく近いところにピンセットの先端を立てて、支点とする
Diamagnetizaion
本電気工学・電子工学専攻にはM1で履修する「特別研修」(通称インターン)と呼ばれる異なる研究室に行って研究を体験する科目があります。
時間割上は木曜日と金曜日の3、4コマで、6週間で研究室が代わり、2つの研究室で研究を経験できることになります。
私が担当するインターンでは、ここ数年は以下のメニューでやっています。
- 前半3週で 超伝導について調査・発表
- 後半3週で 超伝導体単結晶育成
育成した単結晶は磁化と抵抗を測定して超伝導であることを確認しますが、物性量として評価するためには以下の注意が必要です。
磁化
磁化というのは非常にやっかいな物理量で、単位系を理解するのに一苦労です。
ここで使用するQuantum Design社のMagnetic Property Measurement System (MPMS)は磁化の測定値として”EMU”と言う単位でデータファイルに出力します。我々の装置では,”Long Moment”という行です。
物性量にするためには、単位量当たりにする必要があります。一般には質量当たり(つまり、emu/g)がよく用いられますが、測定対象が超伝導体の場合単位体積当たり(emu/cm3)、磁性体の場合式量当たり(emu/f.u.)で計算すると物性がよくわかります。
超伝導体の場合、完全反磁性では体積磁化率は-1/4π となるべきですので、これとの比較を試みます。
測定値を”EMU”だとすると、試料の体積Vを用いると体積磁化はMv=EMU/V、Vをcm3で計算したとき、単位はgauss/cm3となります。
ここで、「あれ?」と思ったかもしれません。いつの間にかemuと言う単位がgaussに変わっています。これは、磁化の値をemuで示すときはCGS-gaussではgaussの意味である、と言うことになっているからです。
体積磁化率を求めるときはこの値をgauss単位の磁場(正確にはOe単位の外部磁場により真空中に誘起される磁束密度)で割ります。
従ってχv=Mv/μ0H[cm-3]となります。
たとえば、V=1.6mmx1.4mmx30
μ mの薄片状の単結晶の薄片に垂直に磁場を加えてH=1Oeの外部磁場により磁化を測定したとき、超伝導転移を示して磁化の値が低温においてEMU=-8×10-3 emuで飽和したとします。このとき、結晶は完全反磁性になったと考えられるので、体積磁化率を出してみましょう。
χv=EMU/(V μ0 H)=-11.9 [cm-3]
を得ますが、これは1/4πよりはるかに大きな値です。この理由は、測定に問題があり、
- 超伝導マグネットを使用しているMPMSの低磁場の制御は再現性が低い(正確に校正する方法はある)
- 薄片に垂直に磁場を加えているので、反磁場効果のため磁化の絶対値が大きくなっている
- 10ガウス以上の磁場で測定する(あるいは低磁場を校正した後測定する)
- 反磁場係数を計算できる形状に試料を整形する
Bibtex database
Bibファイルのパスを通す
従来から論文を書くのに使用していたWinedtとの相性からMiKTEXを導入したところ,bibファイルの移植も必要になりました.
日本語用に従来のTEXシステムを残しているので,両方で文献データベースを使いたい,ということで見つけた方法が
環境変数に
BIBINPUT=bibファイルのパス
を加える,というもの.
これで複数TEXで文献データベースを共有できるようである.
WinEdtのローカル変数としても設定できる
Options/Execution modes/Variables
を参照
PDFのコレクションからbibファイルを作る方法
Mendeleyをダウンロードして,ローカルに保存されたpdfファイルのリストを作成する.
最近のpdfファイルの場合,論文題目,雑誌名,巻号,ページなと基本的な情報は自動的に認識される.
Physical Review 系の雑誌ではarticle numberがページとして認識されないようで、多くの場合page変数が1になるのでMendeleyで修正が必要。
テキスト化されていないpdfファイルでは,テキスト埋め込みを行って再度Mendeleyに登録する.
これらの情報をbibtexの書式で指定のファイル名で保存することができる.
Path, ファイル名の設定はMendeleyのOptions/BibTeXを参照
bibtexデータベースの主キー(texファイルへの引数)は citation key で設定する.
citatoin key は自動的に生成される場合もあり.
Mendeley上でデータを更新しても同一のエントリーがある場合、出力結果に反映されないので、bibファイル上で削除する
Winedt+MikTEX+Bibtex
論文を書くときにはすばらしいツール.(それでも遅筆は直らない)
bibファイルを同時に開いておくと,citation keyの候補が現れる.
pdfコンパイルも一発.
Relaxation time in Drude model
電気伝導を説明する古典的なモデルにDrudeモデルというのがある.
これは,電子が(何かに)散乱されることにより運動エネルギーを失い,ジュール熱になる,というモデルである.
このモデルは正しくないとわかっているのだが,電気伝導を初歩的な概念で説明できるため,量子力学を習う前の電気伝導の説明には良く用いられる.
この電子散乱に関して有名な議論がある.私は勝手に「緩和時間2倍問題」と呼んでいる.
電子の緩和時間を\tauで表すと,散乱されずに残っている電子の割合は\exp(-1/\tau)となる. 最後の散乱から\tau時間経過した電子が散乱されない割合はやはり\exp(-1/\tau)である. そうすると,電子の寿命は2\tauになる.
これは詭弁なのだが,何がおかしいか?
問題は重みを無視していることにある.
ちなみに,Shockleyの有名な教科書「半導体物理学」8.5節で言及されているが日本語訳ではわかりにくい表現である.
それにしてもこの本の内容はすばらしい.絶版となっているのが惜しい.
14章冒頭の記述(川村肇訳 吉岡書店刊)
量子力学は直接の物理的意味を持たない抽象的な数学を用いるので,理論物理学の中でも可成りむつかしい分野の一つと思われている. (中略) そのように直接的の意味づけをもたないことは教育的な見地からは明らかに不利である. しかしこのことは理論を適用したときに正しさに欠けるところがあると云うことには決してならない. 経験科学の数学的理論が満足しなければならない至上要請はそれが実験に合わなければならないということである.
いやはや,実学である物理の真髄です.

![IMG_1340[1]](http://sk.kuee.kyoto-u.ac.jp/ja/wp-content/uploads/2014/06/IMG_13401-e1403924635274-225x300.jpg)
![IMG_1341[1]](http://sk.kuee.kyoto-u.ac.jp/ja/wp-content/uploads/2014/06/IMG_13411-300x225.jpg)