BW状態

超流動³He-B相で実現していると考えられている、「最も等方的な」スピン三重項p波状態であるBalian-Werthamer（BW）状態の模式図（下図）を作ります。ちなみにこの図はこちらのレビュー記事で用いたものです。

BW状態について

ヘリウムの同位体³Heの超流動状態のうち、B相と呼ばれる相内で実現していると考えられているのがBW状態です。BW状態は波数空間の基底\(k_{\mu}=(k_x, k_y, k_z)\)とスピン空間のd-ベクトル（クーパー対のスピンに垂直なベクトル）の基底\(d_{\nu} = (d_x, d_y, d_z)\)をつなぐ行列\(d_{\mu\nu}\)を用いて、 \[ d_{\mu\nu} = \left( \begin{array}{3}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right) \] と表されます。また、より分かりやすく言うと、 \[ \boldsymbol{d}(\boldsymbol{k}) = d_0 \frac{\boldsymbol{k}}{|\boldsymbol{k}|} \] のように「dベクトルと波数が平行な状態」となっています。ただし、より厳密にいうとdベクトルの回転に対して無限の縮退があります。この縮退はスピン軌道相互作用を考慮することで解けて、dベクトルと波数が約109度の方向を成す状態が安定であるといわれています。しかし、ここではこれらの詳細はおいておき、もっとも簡単な\(\boldsymbol{d}\parallel\boldsymbol{k}\)となる状態を模式図にしてみることにしましょう。

上述のように、BW状態は、スピン三重項超伝導状態を表す秩序変数であるdベクトルが強い波数依存性を持っており、さらにdベクトルが3次元的な構造を持っているのが特徴です。このdベクトルの立体的な構造のため、こちらのように波動関数の位相を色で表す方法では波動関数をうまく表現できません。一方で、「dベクトルの方向」を色や矢印で表現することで超伝導状態をうまく図示できます。

なお、この例では図をかっこよく見せるために、開発版gnuplot 5.1以降で採用されているpm3dのlightningオプションを用いています。5.0系またはそれ以前のgnuplotでは使えないのでご注意ください。

BW状態の模式図（矢印無しバージョン）

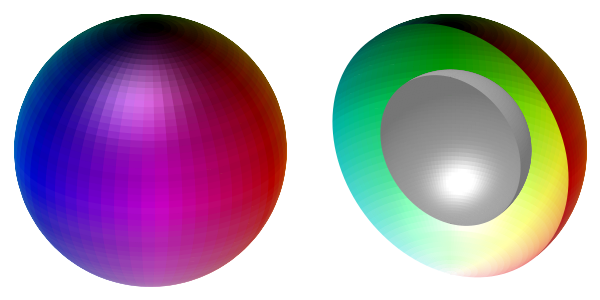
上式であらわされる最もシンプルなBW状態ではdベクトルがFermi波数に平行になっています。dベクトルの方向を\(c\)軸方向に対する極角\(\theta\)と\(ab\)面内の方位角\(\phi\)で表し、それぞれをHSV色空間の明度/彩度と色相で表現することで、ギャップ構造を表現することができます。

以下のようなスクリプトを実行すると、3D-p_BW.pngという画像ファイルが生成されます。この画像では、ギャップの模式図に加えて、それを半分に切った場合の図を並べてあります。

########################## HSVをフルに使うための設定  ######################################

# HSV色空間からRGB色空間への変換。Wikipedia参照
HSV_Hi(h)=sgn(h)*floor(abs(h)/60.0)%6+(h>=0 ? 0 : 5)
HSV_f(h)=(sgn(h)*(abs(h)-(floor(abs(h))/360)*360.0)/60.0+(h>=0 ? 0 : 6))-HSV_Hi(h)
HSV2R(h,s,v)=( \
     HSV_Hi(h)==0 || HSV_Hi(h)==5 ? v                    : (\
     HSV_Hi(h)==1                 ? v*(1-HSV_f(h)*s)     : (\
     HSV_Hi(h)==4                 ? v*(1-(1-HSV_f(h))*s) : (\
     HSV_Hi(h)==2 || HSV_Hi(h)==3 ? v*(1-s)              : 0.0) )))
HSV2G(h,s,v)=( \
     HSV_Hi(h)==1 || HSV_Hi(h)==2 ? v                    : (\
     HSV_Hi(h)==3                 ? v*(1-HSV_f(h)*s)     : (\
     HSV_Hi(h)==0                 ? v*(1-(1-HSV_f(h))*s) : (\
     HSV_Hi(h)==4 || HSV_Hi(h)==5 ? v*(1-s)              : 0.0) )))
HSV2B(h,s,v)=( \
     HSV_Hi(h)==3 || HSV_Hi(h)==4 ? v                    : (\
     HSV_Hi(h)==5                 ? v*(1-HSV_f(h)*s)     : (\
     HSV_Hi(h)==2                 ? v*(1-(1-HSV_f(h))*s) : (\
     HSV_Hi(h)==0 || HSV_Hi(h)==1 ? v*(1-s)              : 0.0) )))

set angles degrees
# HSVサークルの動径方向分割数
N=50.0
colmax = N*360.0

gray2S(gray) = gray >= 0.5 ? (floor((1-gray)*2*colmax/360.0)/N) : 1
gray2V(gray) = gray <= 0.5 ? (floor((gray)*2*colmax/360.0)/N) : 1

set palette model RGB functions \
     HSV2R((gray*colmax/360.0-floor(gray*colmax/360.0))*360.0, gray2S(gray), gray2V(gray)),\
     HSV2G((gray*colmax/360.0-floor(gray*colmax/360.0))*360.0, gray2S(gray), gray2V(gray)),\
     HSV2B((gray*colmax/360.0-floor(gray*colmax/360.0))*360.0, gray2S(gray), gray2V(gray))

set cbrange [0:colmax]

########################## HSVをフルに使うための設定 ここまで ######################################


############# 座標を格納するファイルの作成 ##############################

file = "angle.dat"
file_half = "angle_half.dat"

set urange [360:360+180.]
set vrange [0:360.]
set samples 63
set isosamples 63

set parametric
set zrange [0:1]
set table file
splot u,v,(0)
unset table


set urange [360:360+180.]
set vrange [0:180.]
set samples 63
set isosamples 63
set zrange [0:1]
set table file_half
splot u,v,(0)
unset table

############# 座標を格納するファイルの作成 ここまで ##############################



set term pngcairo size 600,300 font "Arial,12"
set out "3D-p_BW.png"


############# 超伝導ギャップ構造を定義する定数と関数 ##############################

## Fermi端数
kF = 0.3 
## ギャップの大きさ
gap = 0.2 
## Plotする範囲
Range = (kF+gap)*1.1

## ギャップの振幅 
amp(theta,phi) = 1.0
## dベクトルの極角Theta （角度のファイルには360度から540度までが格納されているので、360を引いておく。）
d_angle_t(theta,phi)=theta-360.0 
## dベクトルの方位角Phi
d_angle_p(theta,phi)=phi

## ギャップを書く時の補助関数         
R(theta,phi) = kF + gap*amp(theta,phi)
R0(theta,phi) = kF *0.99

############# 超伝導ギャップ構造を定義する定数と関数 ここまで ##############################

set xrange [-Range:Range]
set yrange [-Range:Range]
set zrange [-Range:Range]

set view 65,30
set view equal xyz
unset key

set border 0
unset xtics
unset ytics
unset ztics

unset colorbox

# pm3d: lightning オプションを含めて設定
set pm3d implicit at s hidden3d depth noborder
set pm3d lighting primary 0.3 specular 0.45
set pm3d corners2color min



set multiplot


### 左半分に、全体像をプロット ###
set tmargin screen 1
set bmargin screen 0
set rmargin screen 0.5
set lmargin screen 0


splot file using (R($1,$2)*sin($1)*cos($2)):(R($1,$2)*sin($1)*sin($2)):(R($1,$2)*cos($1)):\
     (floor(d_angle_t($1,$2)/180.0*N)*360.0+d_angle_p($1,$2)) nosurface


### 左半分に、一部が欠けた像をプロット Fermi面は灰色で ###

set tmargin screen 1
set bmargin screen 0
set rmargin screen 1
set lmargin screen 0.5


splot file_half using (R($1,$2)*sin($1)*cos($2)):(R($1,$2)*sin($1)*sin($2)):(R($1,$2)*cos($1)):\
     (floor(d_angle_t($1,$2)/180.0*N)*360.0+d_angle_p($1,$2)) nosurface,\
      "" using (R0($1,$2)*sin($1)*cos($2)):(R0($1,$2)*sin($1)*sin($2)):(R0($1,$2)*cos($1)):\
     (0xAAAAAA) nosurface lc rgb variable


unset multiplot

BW状態の模式図（矢印ありバージョン）

色でdベクトルの方向を表すのに加えて、矢印でもdベクトルを表示すると、より視覚的にわかりやすくなります。また、dベクトルがヘッジホック型になっている、言い換えると\(k = 0\)に「モノポール」がある場合の電場や磁場の湧き出しと類似の構造をしている、ことも分かります。このような構造は、連続変形だけで消し去ることはできず、トポロジカルに非自明な構造になっています。このため、BW状態は「トポロジカル」な超流動状態にの一つです。

以下のようなスクリプトを実行すると、3D-p_BW_with_arrow.pngという画像ファイルが生成されます。この画像では、ギャップの模式図に加えて、それを半分に切った場合の図を並べてあります。

########################## HSVをフルに使うための設定  ######################################

# HSV色空間からRGB色空間への変換。Wikipedia参照
HSV_Hi(h)=sgn(h)*floor(abs(h)/60.0)%6+(h>=0 ? 0 : 5)
HSV_f(h)=(sgn(h)*(abs(h)-(floor(abs(h))/360)*360.0)/60.0+(h>=0 ? 0 : 6))-HSV_Hi(h)
HSV2R(h,s,v)=( \
     HSV_Hi(h)==0 || HSV_Hi(h)==5 ? v                    : (\
     HSV_Hi(h)==1                 ? v*(1-HSV_f(h)*s)     : (\
     HSV_Hi(h)==4                 ? v*(1-(1-HSV_f(h))*s) : (\
     HSV_Hi(h)==2 || HSV_Hi(h)==3 ? v*(1-s)              : 0.0) )))
HSV2G(h,s,v)=( \
     HSV_Hi(h)==1 || HSV_Hi(h)==2 ? v                    : (\
     HSV_Hi(h)==3                 ? v*(1-HSV_f(h)*s)     : (\
     HSV_Hi(h)==0                 ? v*(1-(1-HSV_f(h))*s) : (\
     HSV_Hi(h)==4 || HSV_Hi(h)==5 ? v*(1-s)              : 0.0) )))
HSV2B(h,s,v)=( \
     HSV_Hi(h)==3 || HSV_Hi(h)==4 ? v                    : (\
     HSV_Hi(h)==5                 ? v*(1-HSV_f(h)*s)     : (\
     HSV_Hi(h)==2                 ? v*(1-(1-HSV_f(h))*s) : (\
     HSV_Hi(h)==0 || HSV_Hi(h)==1 ? v*(1-s)              : 0.0) )))

set angles degrees
# HSVサークルの動径方向分割数
N=50.0
colmax = N*360.0

gray2S(gray) = gray >= 0.5 ? (floor((1-gray)*2*colmax/360.0)/N) : 1
gray2V(gray) = gray <= 0.5 ? (floor((gray)*2*colmax/360.0)/N) : 1

set palette model RGB functions \
     HSV2R((gray*colmax/360.0-floor(gray*colmax/360.0))*360.0, gray2S(gray), gray2V(gray)),\
     HSV2G((gray*colmax/360.0-floor(gray*colmax/360.0))*360.0, gray2S(gray), gray2V(gray)),\
     HSV2B((gray*colmax/360.0-floor(gray*colmax/360.0))*360.0, gray2S(gray), gray2V(gray))


set cbrange [0:colmax]


########################## HSVをフルに使うための設定 ここまで ######################################


############# 座標を格納するファイルの作成 ##############################

file = "angle.dat"
file_half = "angle_half.dat"
file_arrow = "arrow_r-phi.dat"

set urange [360:360+180.]
set vrange [0:360.]
set samples 63
set isosamples 63

set parametric
set zrange [0:1]
set table file
splot u,v,(0)
unset table


set urange [360:360+180.]
set vrange [0:180.]
set samples 63
set isosamples 63
set zrange [0:1]
set table file_half
splot u,v,(0)
unset table

set parametric
set angles degrees
set urange [0:1]
set vrange [0:360]
set samples 40
set isosamples 40

set table file_arrow
splot u,v,0
unset table


############# 座標を格納するファイルの作成 ここまで ##############################


set term pngcairo size 600,300 font "Arial,12"
set out "3D-p_BW_with_arrow.png"


############# 超伝導ギャップ構造を定義する定数と関数 ##############################

## Fermi端数
kF = 0.3 
## ギャップの大きさ
gap = 0.2 
## Plotする範囲
Range = (kF+gap)*1.65

## ギャップの振幅 
amp(theta,phi) = 1.0
## dベクトルの極角Theta （角度のファイルには360度から540度までが格納されているので、360を引いておく。）
d_angle_t(theta,phi)=theta-360.0
## dベクトルの方位角Phi
d_angle_p(theta,phi)=phi

## ギャップを書く時の補助関数         
FS_gap(theta,phi) = kF + gap*amp(theta,phi)
FS(theta,phi) = kF *0.99

############# 超伝導ギャップ構造を定義する定数と関数 ここまで ############################


################ 立体矢印を描くための定数と関数 ##############################

# 矢印のパラメータ
# 矢印の頭（Head）の長さ
HL = gap*0.5
# 矢印の頭（Head）の半径
HR = gap*0.2
# 矢印の軸部分（Body）の長さ
BL = gap*1.1
# 矢印の軸部分（Body）の半径
BR = gap*0.1

# z軸向きの矢印の表面を表す関数 uは円筒座標のz（ただし0-1に規格化）、
# vは円筒座標のthetaに対応。
# R(u)は円筒座標のr
R(u) = (u < (BL/(BL+HL)) ? BR :  ((u-1.0)*(HL+BL)/HL * HR ))
X(u,v)=R(u)*cos(v)
Y(u,v)=R(u)*sin(v)
Z(u,v)=(u)*(HL+BL)

# 矢印を、Eular角alphaとbetaで回転させ、さらに(X0, Y0, Z0) に平行移動
Fx(u,v)=X0+X(u,v)*cos(alpha)+(Y(u,v)*cos(beta)+Z(u,v)*sin(beta))*sin(alpha)
Fy(u,v)=Y0-X(u,v)*sin(alpha)+(Y(u,v)*cos(beta)+Z(u,v)*sin(beta))*cos(alpha)
Fz(u,v)=Z0-Y(u,v)*sin(beta) + Z(u,v)*cos(beta)

# 矢印を描く数を決めるためのパラメータ
Arrow_N = 12
Arrow_M = 7
dTheta = 180./Arrow_M
max(x,y) = (x < y ? y : x)

################ 立体矢印を描くための定数と関数 ここまで ##############################


set xrange [-Range:Range]
set yrange [-Range:Range]
set zrange [-Range:Range]

set view 65,30
set view equal xyz
unset key

set border 0
unset xtics
unset ytics
unset ztics

unset colorbox


# pm3d: lightning オプションを含めて設定
set pm3d implicit at s hidden3d depth noborder
set pm3d lighting primary 0.3 specular 0.45
set pm3d corners2color min


set multiplot






### 左半分に、全体像をプロット ###
set tmargin screen 1
set bmargin screen 0
set rmargin screen 0.5
set lmargin screen 0

splot file using (FS_gap($1,$2)*sin($1)*cos($2)):(FS_gap($1,$2)*sin($1)*sin($2)):(FS_gap($1,$2)*cos($1)):\
     (floor(d_angle_t($1,$2)/180.0*N)*360.0+d_angle_p($1,$2)) nosurface,\
     for [i=1:Arrow_N*Arrow_M]\
     j = i%Arrow_N, k = i/Arrow_N, Theta = dTheta*k, jmax = max(floor(Arrow_N*sin(Theta)),1),\
     dPhi = 360.0/jmax, Phi = j*dPhi, alpha = 90-Phi, beta = Theta,\
     X0=FS_gap(Theta,Phi)*sin(Theta)*cos(Phi), Y0=FS_gap(Theta,Phi)*sin(Theta)*sin(Phi), Z0=FS_gap(Theta,Phi)*cos(Theta), \
     file_arrow using (j<=jmax ? Fx($1,$2) : 1/0):(Fy($1,$2)):(Fz($1,$2)):(floor(d_angle_t(Theta+360,Phi)/180.0*N)*360.0+d_angle_p(Theta+360,Phi)) nosurface,\




### 左半分に、一部が欠けた像をプロット Fermi面は灰色で ###

set tmargin screen 1
set bmargin screen 0
set rmargin screen 1
set lmargin screen 0.5

Arrow_N = 6
splot file_half using (FS_gap($1,$2)*sin($1)*cos($2)):(FS_gap($1,$2)*sin($1)*sin($2)):(FS_gap($1,$2)*cos($1)):\
     (floor(d_angle_t($1,$2)/180.0*N)*360.0+d_angle_p($1,$2)) nosurface,\
     file_half using (FS($1,$2)*sin($1)*cos($2)):(FS($1,$2)*sin($1)*sin($2)):(FS($1,$2)*cos($1)):\
     (0xAAAAAA) nosurface lc rgb variable,\
     for [i=1:Arrow_N*Arrow_M]\
     j = i%Arrow_N, k = i/Arrow_N, Theta = dTheta*k, jmax = max(floor(Arrow_N*sin(Theta)),1),\
     dPhi = 180.0/jmax, Phi = j*dPhi, alpha = 90-Phi, beta = Theta,\
     X0=FS_gap(Theta,Phi)*sin(Theta)*cos(Phi), Y0=FS_gap(Theta,Phi)*sin(Theta)*sin(Phi), Z0=FS_gap(Theta,Phi)*cos(Theta), \
     file_arrow using (j<=jmax ? Fx($1,$2) : 1/0):(Fy($1,$2)):(Fz($1,$2)):(floor(d_angle_t(Theta+360,Phi)/180.0*N)*360.0+d_angle_p(Theta+360,Phi)) nosurface,\

unset multiplot