Last updated: Sep. 27, 2010

You're th visitor.

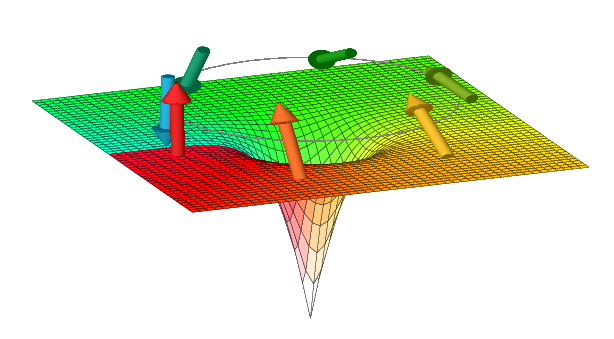
半整数渦糸

こちらを応用し、スピン3重項超伝導・超流動において実現が予言されている「半整数量子化渦糸」の模式図を作りました。矢印はdベクトルと呼ばれるスピン部分の位相を、また底面の色は軌道部分の位相をそれぞれ表します。渦糸周りを一周したときに、スピン部分と軌道部分の位相がそれぞれπだけずれることで全体としては2πだけ位相がずれて全体の波動関数の一価性を保ちます。

上図は下のスクリプトを実行して作られたPostScriptファイルhalf-vortex.epsからコピーしたものです。

#version 4.4.0

set angles degrees


MODE = "PRINT"


# 光の方向
sx=1.0
sy=1.0
sz=-1.0

# 微分用の微小数
h=0.000001

# Fx,Fy,Fzのuおよびvによる偏微分
dFxu(u,v)=(Fx(u+h,v)-Fx(u-h,v))/(2.0*h)
dFyu(u,v)=(Fy(u+h,v)-Fy(u-h,v))/(2.0*h)
dFzu(u,v)=(Fz(u+h,v)-Fz(u-h,v))/(2.0*h)
dFxv(u,v)=(Fx(u,v+h)-Fx(u,v-h))/(2.0*h)
dFyv(u,v)=(Fy(u,v+h)-Fy(u,v-h))/(2.0*h)
dFzv(u,v)=(Fz(u,v+h)-Fz(u,v-h))/(2.0*h)

# 法線ベクトルの各成分 n = lu x lv
nx(u,v)=dFyu(u,v)*dFzv(u,v)-dFyv(u,v)*dFzu(u,v)
ny(u,v)=dFzu(u,v)*dFxv(u,v)-dFzv(u,v)*dFxu(u,v)
nz(u,v)=dFxu(u,v)*dFyv(u,v)-dFxv(u,v)*dFyu(u,v)

# 光の方向ベクトルsの長さ
s_length=sqrt(sx**2+sy**2+sz**2)
# 法線ベクトルnの長さ
n_length(u,v)=sqrt(nx(u,v)**2+ny(u,v)**2+nz(u,v)**2)

# 光の方向ベクトルsと表面の法線ベクトルnの内積で色を決める
light(u,v)=(n_length(u,v)!=0.0 ? \
           (sx*nx(u,v)+sy*ny(u,v)+sz*nz(u,v))/(s_length*n_length(u,v)) :\
           light(u+h,v+h))



## HSV色空間からRGB色空間への変換。Wikipedia参照
#変換の補助関数群
HSV_Hi(h)=sgn(h)*floor(abs(h)/60)%6+(h>=0 ? 0 : 5)
HSV_f(h)=(sgn(h)*(abs(h)-(floor(abs(h))/360)*360.0)/60.0+(h>=0 ? 0 : 6))-HSV_Hi(h)
HSV2R(h,s,v)=( \
     HSV_Hi(h)==0 || HSV_Hi(h)==5 ? v                    : (\
     HSV_Hi(h)==1                 ? v*(1-HSV_f(h)*s)     : (\
     HSV_Hi(h)==4                 ? v*(1-(1-HSV_f(h))*s) : (\
     HSV_Hi(h)==2 || HSV_Hi(h)==3 ? v*(1-s)              : 0.0) )))
HSV2G(h,s,v)=( \
     HSV_Hi(h)==1 || HSV_Hi(h)==2 ? v                    : (\
     HSV_Hi(h)==3                 ? v*(1-HSV_f(h)*s)     : (\
     HSV_Hi(h)==0                 ? v*(1-(1-HSV_f(h))*s) : (\
     HSV_Hi(h)==4 || HSV_Hi(h)==5 ? v*(1-s)              : 0.0) )))
HSV2B(h,s,v)=( \
     HSV_Hi(h)==3 || HSV_Hi(h)==4 ? v                    : (\
     HSV_Hi(h)==5                 ? v*(1-HSV_f(h)*s)     : (\
     HSV_Hi(h)==2                 ? v*(1-(1-HSV_f(h))*s) : (\
     HSV_Hi(h)==0 || HSV_Hi(h)==1 ? v*(1-s)              : 0.0) )))
     
#HSV色空間のパラメータh,s,vをRGBの色を表す16進数文字列"#rrggbb"に変換する。
#3番目の引数の係数が200になっているのは、
#Greenを255にすると明るすぎて紙面上や画面上で見づらいため。
HSV2RGB(h,s,v)=sprintf("#%02x%02x%02x", \
               255*HSV2R(h,s,v), 200*HSV2G(h,s,v), 255*HSV2B(h,s,v))

#整数nをRGB文字列"#rrggbb"に変換する。
period=60.0   #グラデーションの周期（360で色が一周する）
start=0.0     #グラデーションをスタートする色。0ならn=0は赤に対応する。
num2color(n)=HSV2RGB(360.0*n/period+start, 1.0, 1.0)




set xrange [-0.1:0.1]
set yrange [-0.1:0.1]
set samples 101
set isosamples 101

# いったんパラメータファイルを作る
tablefile="table3.dat"
set table tablefile
splot 0
unset table



N = 40.0

set parametric
set angles degrees
set urange [0:1]
set vrange [0:360]
set samples N
set isosamples N

# いったんパラメータファイルを作る
tablefile2="table_polar.dat"
set table tablefile2
splot u,v,0
unset table

unset parametric

Size = 1.0
xmax = 0.05
ymax = 0.05
zmax = 0.7
set xrange [-Size:Size]
set yrange [-Size:Size]
set zrange [0:2*Size]

set pm3d depthorder interpolate 1,1 hidden3d 1
set style line 1  linetype 1 linecolor rgb "black" linewidth 0.25
set view 65,338
set hidden3d

unset colorbox
set border 0
unset xtics 
unset ytics 
unset ztics
unset key


N=50.0
colmax = (N)*360.0

set cbrange [0:colmax]
#set zrange [0:colmax]

# 色使いの指定 渦芯が白い
set palette model RGB functions \
     HSV2R((gray*colmax/360.0-floor(gray*colmax/360.0))*360.0, \
           (floor(gray*colmax/360.0)/N), 1),\
     HSV2G((gray*colmax/360.0-floor(gray*colmax/360.0))*360.0, \
           (floor(gray*colmax/360.0)/N), 1),\
     HSV2B((gray*colmax/360.0-floor(gray*colmax/360.0))*360.0, \
           (floor(gray*colmax/360.0)/N), 1)

# 色使いの指定 渦芯が黒い
set palette model RGB functions \
     HSV2R((gray*colmax/360.0-floor(gray*colmax/360.0))*360.0, 1, \
           (floor(gray*colmax/360.0)/N)),\
     HSV2G((gray*colmax/360.0-floor(gray*colmax/360.0))*360.0, 1, \
           (floor(gray*colmax/360.0)/N)),\
     HSV2B((gray*colmax/360.0-floor(gray*colmax/360.0))*360.0, 1, \
           (floor(gray*colmax/360.0)/N))


set pm3d corners2color min 

set multiplot

# 表面の媒介変数関数
vortex(u,v)=tanh(nu*sqrt(u**2+v**2)/xi)
nu=1.0
xi=0.01

splot tablefile using ($1/xmax*Size):($2/ymax*Size):(vortex($1,$2)/zmax*Size):\
                      (floor(vortex($1,$2)*N)*360.0+atan2($2,$1)*0.5+90) \
                       with pm3d



# 色使いの指定
set pm3d depthorder interpolate 3,3  nohidden3d
set cbrange [0:1]


# 矢印のパラメータ
HL = 0.15
HR = 0.05
HR = 0.07
BL = 0.4
BR = 0.02
BR = 0.03
Base = 1.7

D = 1/N
R(u) = (u < (BL/(BL+HL)) ? BR :  ((u-1.0)*(HL+BL)/HL * HR ))
X(u,v)=R(u)*cos(v)
Y(u,v)=R(u)*sin(v)
Z(u,v)=(u-0.5)*(HL+BL)

Fx(u,v)=X0+X(u,v)*cos(alpha)+(Y(u,v)*cos(beta)+Z(u,v)*sin(beta))*sin(alpha)
Fy(u,v)=Y0-X(u,v)*sin(alpha)+(Y(u,v)*cos(beta)+Z(u,v)*sin(beta))*cos(alpha)
Fz(u,v)=Z0-Y(u,v)*sin(beta) + Z(u,v)*cos(beta)


# リングの太さ
AR = 0.7

set parametric
set vrange [0:360]
splot AR*cos(v),AR*sin(v),Base w l lt 1 lc rgb "gray50"
unset parametric

Phi = 355.0
alpha = 0.0

X0=AR*cos(Phi + 180)
Y0=AR*sin(Phi + 180)
Z0=Base
beta = Phi*0.5
set palette defined ( 0 HSV2RGB(Phi*0.5, 1.0, 0.5) , 1 HSV2RGB(Phi*0.5, 0.8, 1.0))
splot tablefile2 using (Fx($1,$2)):(Fy($1,$2)):(Fz($1,$2)):(light($1,$2)) with pm3d

Phi = 60.0
X0=AR*cos(Phi + 180)
Y0=AR*sin(Phi + 180)
Z0=Base
beta = Phi*0.5
set palette defined ( 0 HSV2RGB(Phi*0.5, 1.0, 0.5) , 1 HSV2RGB(Phi*0.5, 0.8, 1.0))
splot tablefile2 using (Fx($1,$2)):(Fy($1,$2)):(Fz($1,$2)):(light($1,$2)) with pm3d


Phi = 120.0
X0=AR*cos(Phi + 180)
Y0=AR*sin(Phi + 180)
Z0=Base
beta = Phi*0.5
set palette defined ( 0 HSV2RGB(Phi*0.5, 1.0, 0.5) , 1 HSV2RGB(Phi*0.5, 0.8, 1.0))
splot tablefile2 using (Fx($1,$2)):(Fy($1,$2)):(Fz($1,$2)):(light($1,$2)) with pm3d


Phi = 180.0
X0=AR*cos(Phi + 180)
Y0=AR*sin(Phi + 180)
Z0=Base
beta = Phi*0.5
set palette defined ( 0 HSV2RGB(Phi*0.5, 1.0, 0.5) , 1 HSV2RGB(Phi*0.5, 0.8, 1.0))
splot tablefile2 using (Fx($1,$2)):(Fy($1,$2)):(Fz($1,$2)):(light($1,$2)) with pm3d


Phi = 240.0
X0=AR*cos(Phi + 180)
Y0=AR*sin(Phi + 180)
Z0=Base
beta = Phi*0.5
set palette defined ( 0 HSV2RGB(Phi*0.5, 1.0, 0.5) , 1 HSV2RGB(Phi*0.5, 0.8, 1.0))
splot tablefile2 using (Fx($1,$2)):(Fy($1,$2)):(Fz($1,$2)):(light($1,$2)) with pm3d

Phi = 300.0
X0=AR*cos(Phi + 180)
Y0=AR*sin(Phi + 180)
Z0=Base
beta = Phi*0.5
set palette defined ( 0 HSV2RGB(Phi*0.5, 1.0, 0.5) , 1 HSV2RGB(Phi*0.5, 0.8, 1.0))
splot tablefile2 using (Fx($1,$2)):(Fy($1,$2)):(Fz($1,$2)):(light($1,$2)) with pm3d

Phi = 5.0
X0=AR*cos(Phi + 180)
Y0=AR*sin(Phi + 180)
Z0=Base
beta = Phi*0.5
set palette defined ( 0 HSV2RGB(Phi*0.5, 1.0, 0.5) , 1 HSV2RGB(Phi*0.5, 0.8, 1.0))
splot tablefile2 using (Fx($1,$2)):(Fy($1,$2)):(Fz($1,$2)):(light($1,$2)) with pm3d


unset multiplot


if (MODE eq "PRINT" && (exist("TERM")==0 || TERM eq "WIN")) \
     pause -1;\
     TERM = "PS";\
     set term post color enhanced;\
     set out "half-vortex.eps";\
     reread

set out
set term pop 
undefine TERM

なお、上のスクリプトにはset palette...が2か所ありますが、あとの方を削除すると下のように渦芯の白いVortexが描けます。

• トップページ
• 自己紹介・経歴
• 研究紹介
  • 最近の成果
• 論文・学会発表
  • 論文リスト
  • 発表リスト
• 教育
  • 教育
  • 課題研究Q4
  • 課題演習B4
• アウトリーチ
• プログラミング
  • xyzzy
    • wgnuplot-mode
    • kyotex-mode
    • eng-comp
  • gnuplot
  • JavaScript
    • プレゼンタイマー
• その他
  • リンク集
  • ニュース一覧
  • 更新履歴
• English Top Page