gnuplotでの配列（もどき）の使用

gnuplot 5.2.0以降では本物の配列が使えるようになったので、ほとんどの場合、この項の内容を使うべき場合はありません。配列の使い方に関してはこちらをご覧下さい。

現在（2015年2月、Version 5.0.0）のところ、gnuplotでは配列を使うことはできません。しかし、関数定義を工夫することで、配列のように使えるものを作ることはできます。ここではその使い方を説明します。

目標
配列（もどき）の実装方法（要素が2つの場合）
配列（もどき）の実装方法（任意個数の要素の場合）
使用例1 - 数値の配列
使用例2 - 文字列の配列
使用例3 - ファイルのデータを配列に保存する
使用例4 - データの線形補間

目標

c言語など、多くの言語では配列を使うことができます。配列とは、整数のindexによって値を参照したり代入したりできるものです。例えば、c言語では以下のように配列を使うことができます。

a[0]=1.0 /* 数値の代入 */

x = a[1] /* 数値の参照 */

通常の変数との大きな違いは、以下のようにindexを利用して繰り返しなどが容易に記述できる点でしょう。

for (i=0; i<10; i++) {sum = sum + a[i];}  /* 繰り返し */

ここでの目標は、上で述べたような機能を使用できるようにすることです。

配列（もどき）の実装方法（要素が2つの場合）

まず、簡単のために2つの要素だけを持つ配列（もどき）を作るにはどうすればいいか考えてみましょう。配列のデータは_a0と_a1という二つの変数に格納します。indexを指定して値を代入するには、以下のような関数a_set(i,val)を定義すれば可能です。

a_set(i, val) = (int(i)==0 ? _a0=val : (int(i)==1 ? _a1=val : 1/0))

ここでは、三項演算子を用いて、indexであるiの値に応じた条件分岐を作り、int(i)が0の場合は_a0に、int(i)が1の場合は_a1に、それぞれ値を代入します。int(i)が0と1以外の場合の時は、1/0を返す（つまりエラーが起こる）ようにしています。

実際、以下のようなスクリプトで、値の代入ができていることは確認できます。なお、gnuplotでは関数呼び出しだけの文はエラーになるので、適当なダミー変数（以下の例ではdummy）への代入文という形をとっています。

a_set(i, val) = (int(i)==0 ? _a0=val : (int(i)==1 ? _a1=val : 1/0))
dummy = a_set(0, 100)
dummy = a_set(1, 200)
print _a0, _a1

これを実行すると、変数_a0には100という値が、変数_a1には200という値が、それぞれ格納されていることがわかります。

次に、配列データをindexを用いて参照する関数a_get(i)を作りましょう。これは、以下のようにして実現できます。

a_get(i) = (int(i)==0 ? _a0 : (int(i)==1 ? _a1 : 1/0))

これも、先ほどと同様、三項演算子を用いた条件分岐で、参照するデータを決めています。

要素が二つでは全くありがたみがないですが、これらが配列（もどき）実装の基本原理です。

配列（もどき）の実装方法（任意の個数の要素の場合）

さて、上で述べた条件分岐を増やしていけば、原理的には任意（と言っても後述のように上限あり）の個数の要素の配列もどきを作れることになります。例えば、要素が5個の場合は以下のようにすればよいことになります。

a_get(i) = (int(i)==0 ? _a0 :(int(i)==1 ? _a1 :(int(i)==2 ? _a2 :(int(i)==3 ? _a3 :(int(i)==4 ? _a4 :1/0)))))
a_set(i,x) = (int(i)==0 ? _a0=x :(int(i)==1 ? _a1=x :(int(i)==2 ? _a2=x :(int(i)==3 ? _a3=x :(int(i)==4 ? _a4=x :1/0)))))

しかし、いちいちこのような関数定義を書き下すのは非常に面倒です。特に、要素がさらに多くなればなるほど、関数定義は煩雑になります。

そこで、do forを用いた繰り返しとevalを用いて、関数定義自体をスクリプトで生成してしまいましょう。evalは、後に続く文字列をgnuplotの命令だと思って実行するコマンドです。具体的には、以下のようにします。

ASIZE= 10  # 配列のサイズ

# 配列にデータを格納する関数a_setを定義するための文字列の生成
str = "a_set(i,x) = "
do for [n=0:ASIZE-1] {str = str . sprintf("(int(i)==%d ? _a%d=x :", n, n)}
str = str. "1/0"
do for [n=0:ASIZE-1] {str = str . ")"}
# 文字列をgnuplotコマンドとして実行
eval str

# 配列のデータを参照する関数a_getを定義するための文字列の生成
str = "a_get(i) = "
do for [n=0:ASIZE-1] {str = str . sprintf("(int(i)==%d ? _a%d :", n, n) }
str = str. "1/0"
do for [n=0:ASIZE-1] {str = str . ")"}
# 文字列をgnuplotコマンドとして実行
eval str

これらを実行すると、ASIZEで決めたサイズの配列もどきへの格納と参照を行うa_set(i,x)とa_get(i)が自動的に定義できます。

例えば、以下の例を実行すると、サイズ100の配列もどきが使えるようになっていることが確かにわかります。

ASIZE= 100  # 配列のサイズ

# 配列にデータを格納する関数a_setを定義するための文字列の生成
str = "a_set(i,x) = "
do for [n=0:ASIZE-1] {str = str . sprintf("(int(i)==%d ? _a%d=x :", n, n)}
str = str. "1/0"
do for [n=0:ASIZE-1] {str = str . ")"}
# 文字列をgnuplotコマンドとして実行
eval str

# 配列のデータを参照する関数a_getを定義するための文字列の生成
str = "a_get(i) = "
do for [n=0:ASIZE-1] {str = str . sprintf("(int(i)==%d ? _a%d :", n, n) }
str = str. "1/0"
do for [n=0:ASIZE-1] {str = str . ")"}
# 文字列をgnuplotコマンドとして実行
eval str

# 値の代入
do for [i=0:ASIZE-1] {dummy=a_set(i,i*100)} 

# 値の表示
do for [i=0:ASIZE-1] {print "a[", i, "] = ", a_get(i)}

ちなみに、筆者の環境（Win8.1 + gnuplot5.0.0本家版）では、以下のようにサイズ5000程度の配列もどきは作ることができましたが、サイズ10000だとエラーが出ました。

使用例1 - 数値の配列

ここでは、有名なフィボナッチ数列を取り上げてみましょう。

フィボナッチ数列F_nは以下のような漸化式で定義されます。

ASIZE=20
# 配列にデータを格納する関数a_setを定義するための文字列の生成
str = "a_set(i,x) = "
do for [n=0:ASIZE-1] {str = str . sprintf("(int(i)==%d ? _a%d=x :", n, n)}
str = str. "1/0"
do for [n=0:ASIZE-1] {str = str . ")"}
# 文字列をgnuplotコマンドとして実行
eval str

# 配列のデータを参照する関数a_getを定義するための文字列の生成
str = "a_get(i) = "
do for [n=0:ASIZE-1] {str = str . sprintf("(int(i)==%d ? _a%d :", n, n) }
str = str. "1/0"
do for [n=0:ASIZE-1] {str = str . ")"}
# 文字列をgnuplotコマンドとして実行
eval str

# フィボナッチ数列を定義する
dummy = a_set(0,0)
dummy = a_set(1,1)
do for [i=2:ASIZE-1]{
     dummy = a_set(i, a_get(i-1)+a_get(i-2))
     }

set boxwidth 0.5 relative
set style fill solid 1.0
offset = 120  # 数値の表示位置のy方向オフセット
set xrange [-1:ASIZE]
set title "Fibonacci numbers" font ",15"

plot sample \
     [n=0:ASIZE-1] "+" using ($0):(a_get($0)) w boxes notitle,\
     [n=0:ASIZE-1] "+" using ($0):(a_get($0)+offset):(sprintf("%d", a_get($0))) w labels notitle

上記の例では、途中で漸化式を用いてフィボナッチ数列を定義しています。また、その結果をプロットする際には、疑似ファイル"+"と、gnuplot 5.0で取り入れられたサンプリング範囲指定のキーワードsampleを使います。

このスクリプトの実行結果は以下のようになり、フィボナッチ数列（0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, ... Wikipediaより）がきちんと計算できていることがわかります。

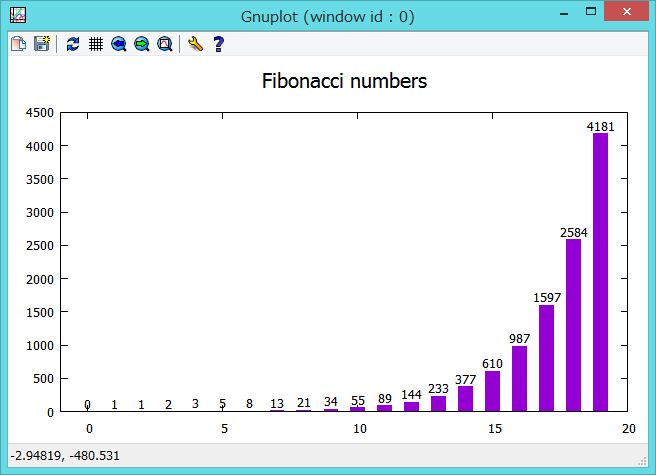
また、フィボナッチ数列は、n番目とn-1番目の数列の要素の比を取ると、黄金比に収束していくことが知られています:

以下のスクリプトを実行すると、確かに、上記の関係が成り立っていることがわかります。

ASIZE=50
# 配列にデータを格納する関数a_setを定義するための文字列の生成
str = "a_set(i,x) = "
do for [n=0:ASIZE-1] {str = str . sprintf("(int(i)==%d ? _a%d=x :", n, n)}
str = str. "1/0"
do for [n=0:ASIZE-1] {str = str . ")"}
# 文字列をgnuplotコマンドとして実行
eval str

# 配列のデータを参照する関数a_getを定義するための文字列の生成
str = "a_get(i) = "
do for [n=0:ASIZE-1] {str = str . sprintf("(int(i)==%d ? _a%d :", n, n) }
str = str. "1/0"
do for [n=0:ASIZE-1] {str = str . ")"}
# 文字列をgnuplotコマンドとして実行
eval str

# フィボナッチ数列を定義する
dummy = a_set(0,0.0)
dummy = a_set(1,1.0)
do for [i=2:ASIZE-1]{
     dummy = a_set(i, a_get(i-1)+a_get(i-2))
     }

set title "Ratio of neighboring Fibonacci numbers" font ",15"

set xrange [0:ASIZE]
plot sample \
     [n=1:ASIZE-1] "+" using ($0):(a_get($0)/a_get($0-1)) w lp notitle,\
     (sqrt(5)+1)*0.5 w l dt "."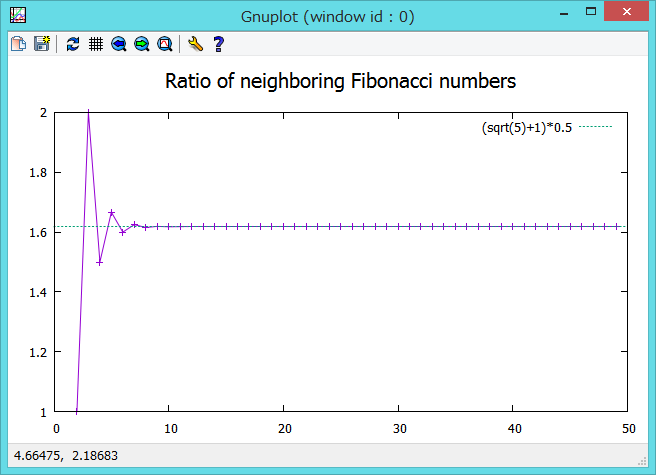

使用例2 - 文字列の配列

この配列もどきは文字列を要素に取ることもできます。gnuplotでは、もともとword()関数を使えば文字列配列に類似のものが使えたのですが、word()関数はスペースを単語区切りとみなしてしまうためにスペースを含むような文字列は適切に扱えませんでした。配列もどきを使えば、スペースを含む文字列でも一つの要素として扱うことができます。

以下の例では、マザーグースの「ロンドン橋落ちた」の詩の各行を要素とする配列もどきを定義して、それをdo forとset labelを使って出力しています。（set border 0以下は完全に遊びです）

ASIZE = 4
# 配列にデータを格納する関数a_setを定義するための文字列の生成
str = "a_set(i,x) = "
do for [n=0:ASIZE-1] {str = str . sprintf("(int(i)==%d ? _a%d=x :", n, n)}
str = str. "1/0"
do for [n=0:ASIZE-1] {str = str . ")"}
# 文字列をgnuplotコマンドとして実行
eval str

# 配列のデータを参照する関数a_getを定義するための文字列の生成
str = "a_get(i) = "
do for [n=0:ASIZE-1] {str = str . sprintf("(int(i)==%d ? _a%d :", n, n) }
str = str. "1/0"
do for [n=0:ASIZE-1] {str = str . ")"}
# 文字列をgnuplotコマンドとして実行
eval str

dummy = a_set(0, "London Bridge is broken down,")
dummy = a_set(1, "Broken down, broken down.")
dummy = a_set(2, "London Bridge is broken down,")
dummy = a_set(3, "My fair lady.")

do for [i=0:3]{
     set label i+1 at graph 0.5,0.8-0.1*i center a_get(i) font ",20"
     }

set border 0
unset xtics
unset ytics
set format xy ""
do for [i=-19:19]{
     set arrow i+20 from first i*0.05, 0.2-0.2*(i*0.05)**2 to first i*0.05, 0.3-0.2*(i*0.05)**2 lw 5 lc rgb "brown" nohead
     }
plot [-1:1][0:1] \
     0.2-0.2*x**2 w l lc rgb "gray40" lw 20 notitle,\
     0.3-0.2*x**2 w l lc rgb "brown" lw 10 notitle

この例の実行結果は以下の通りです。

よりまともな例として、スペースを含むファイル名を扱う場合を紹介したいと思います。以下の例では、空白を含む名前を持つファイルcalculated data A.dat...calculated data D.datのファイル名を配列もどきに格納して、plot forを使ってプロットしています。

# ファイルの生成
sinc(x)=sin(x)/x
set table "calculated data A.dat"
plot sinc(x)
set table "calculated data B.dat"
plot sinc(x*2)
set table "calculated data C.dat"
plot sinc(x*3)
set table "calculated data D.dat"
plot sinc(x*4)
unset table


ASIZE = 4
# 配列にデータを格納する関数a_setを定義するための文字列の生成
str = "a_set(i,x) = "
do for [n=0:ASIZE-1] {str = str . sprintf("(int(i)==%d ? _a%d=x :", n, n)}
str = str. "1/0"
do for [n=0:ASIZE-1] {str = str . ")"}
# 文字列をgnuplotコマンドとして実行
eval str

# 配列のデータを参照する関数a_getを定義するための文字列の生成
str = "a_get(i) = "
do for [n=0:ASIZE-1] {str = str . sprintf("(int(i)==%d ? _a%d :", n, n) }
str = str. "1/0"
do for [n=0:ASIZE-1] {str = str . ")"}
# 文字列をgnuplotコマンドとして実行
eval str

dummy = a_set(0, "calculated data A.dat")
dummy = a_set(1, "calculated data B.dat")
dummy = a_set(2, "calculated data C.dat")
dummy = a_set(3, "calculated data D.dat")

plot for [i=0:3] a_get(i) w l title a_get(i)

このスクリプトの実行例は以下のようになります。word()関数ではうまく扱えなかったスペースを含むファイル名でも、適切に扱えていることがわかります。

使用例3 - ファイルのデータを配列に保存

ファイルの情報を得るためのstatsコマンドと、do forによるループを併用することで、ファイルのデータを配列もどきに保存することができます。

以下の例では、data.datというファイル（これはガウシアン関数をset tableを用いて打ち出したものです）の内容を読み出して、二つの配列xとyに格納する方法を示しています。ファイルの情報を読み出すには、everyオプションを用いて、statsコマンドをデータファイルのある1行にのみ適用するという方法をとっています。こうすると、その行のデータの平均値がSTATS_mean_xやSTATS_mean_yという変数に格納されますが、そもそもデータは1つなので、格納されているデータはその行のデータそのものと等しくなります。

file = "data.dat"

# ファイルの情報を読み出す
stats file using 0 nooutput
FILESIZE = STATS_records

# 配列xにデータを格納する関数x_setを定義するための文字列の生成と実行
str = "x_get(n) = "
do for [i=0:FILESIZE] {str = str . sprintf("(int(n)==%d ? _x%d :", i, i) }
str = str. "1/0"
do for [i=0:FILESIZE] {str = str . ")"}
eval str

# 配列xのデータを読みだす関数x_getを定義するための文字列の生成と実行
str = "x_set(n,x) = "
do for [i=0:FILESIZE] {str = str . sprintf("(int(n)==%d ? (_x%d=x, 0) :", i, i)}
str = str. "1"
do for [i=0:FILESIZE] {str = str . ")"}
eval str


# 配列yにデータを格納する関数y_setを定義するための文字列の生成と実行
str = "y_get(n) = "
do for [i=0:FILESIZE] {str = str . sprintf("(int(n)==%d ? _y%d :", i, i) }
str = str. "1/0"
do for [i=0:FILESIZE] {str = str . ")"}
eval str

# 配列yのデータを読みだす関数y_getを定義するための文字列の生成と実行
str = "y_set(n,x) = "
do for [i=0:FILESIZE] {str = str . sprintf("(int(n)==%d ? (_y%d=x, 0) :", i, i)}
str = str. "1"
do for [i=0:FILESIZE] {str = str . ")"}
eval str

# データを配列に格納する
do for [i=0:FILESIZE-1] {\
     stats "data.dat" using 1:2 every ::i::i nooutput
     dummy=x_set(i,STATS_mean_x)
     dummy=y_set(i,STATS_mean_y)
     }

# 配列のテスト
plot sample [i=0:FILESIZE-1] "+" using (x_get($0)):(y_get($0)) w p pt 5 title "array",\
     "data.dat" using 1:2 w p pt 1 ps 2 lc rgb "red" title "raw data"

この実行結果は以下のようになり、確かにデータファイルの内容が配列もどきに格納されていることがわかります。

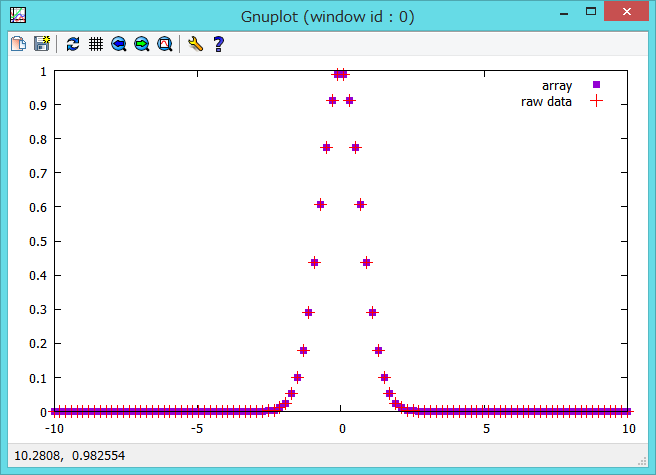
使用例4 - データの線形補間

上記の例をさらに発展させると、データファイルのデータを線形補間した関数を定義することができます:

file = "data.dat"

stats file using 0 nooutput
FILESIZE = STATS_records


# define function x_get(n)
str = "x_get(n) = "
do for [i=0:FILESIZE] {str = str . sprintf("(int(n)==%d ? _x%d :", i, i) }
str = str. "1/0"
do for [i=0:FILESIZE] {str = str . ")"}
eval str

# define function x_set(n,x)
str = "x_set(n,x) = "
do for [i=0:FILESIZE] {str = str . sprintf("(int(n)==%d ? (_x%d=x, 0) :", i, i)}
str = str. "1"
do for [i=0:FILESIZE] {str = str . ")"}
eval str


# define function y_get(n)
str = "y_get(n) = "
do for [i=0:FILESIZE] {str = str . sprintf("(int(n)==%d ? _y%d :", i, i) }
str = str. "1/0"
do for [i=0:FILESIZE] {str = str . ")"}
eval str

# define function y_set(n,x)
str = "y_set(n,x) = "
do for [i=0:FILESIZE] {str = str . sprintf("(int(n)==%d ? (_y%d=x, 0) :", i, i)}
str = str. "1"
do for [i=0:FILESIZE] {str = str . ")"}
eval str

# データファイルの内容を配列xとyとへ格納
do for [i=0:FILESIZE-1] {\
     stats "data.dat" using 1:2 every ::i::i nooutput
     dummy=x_set(i,STATS_mean_x)
     dummy=y_set(i,STATS_mean_y)
     }

# 線形補間した関数 xy_itp(x) を定義
str = "xy_itp(x) = "
do for [i=1:FILESIZE-1] {str = str . sprintf("(x < x_get(%d) ? y_get(%d-1) + (y_get(%d)-y_get(%d-1))/(x_get(%d)-x_get(%d-1))*(x-x_get(%d-1)):", i, i, i, i, i, i, i) }
str = str. "1/0"
do for [i=1:FILESIZE-1] {str = str . ")"}
eval str

set samples 1000
set xrange [x_get(0):x_get(FILESIZE-1)]
plot xy_itp(x), "data.dat" w p

この例の実行結果は以下のようになります。

以下のように拡大してみるとわかりやすいですが、xy_itp(x)は、確かにデータファイルのデータの間を線形補間した関数になっています。

ここで重要なのは、xy_itp(x)関数は、gnuplotの関数になっているため、Fittingをはじめとした様々な用途に使えるという点です。つまり、例えば数値計算でしか得られない関数を実験データに対してFittingしたい場合などに有効になると考えられます。